Multiple Linear Regression

Last updated on May 28, 2020 5 min read R

Linear Regression is using a straight line to describe a relationship between variables. It finds the best possible fit through minimizing “error” of the model. Simple linear regression uses one independent variable and one dependent variable and multiple linear regression uses more than one independent variable with one dependent variable. Multivariate linear regression uses more than one dependent variable. I most often use multiple linear regression so I’ll discuss that here.

1. Load your packages

library(ggplot2)
library(dplyr)
library(broom)
library(ggpubr)
library(moderndive)
library(readr)
library(readxl)
library(skimr)
library(tidyverse)

2. Load the data

data = read_xls("PS206767-553247439.xls", sheet = 2)
data = data %>% 
  select(1, 4, 10, 39) %>% 
  mutate(height = as.numeric(`Height (cm)`), 
         dose = as.numeric(`Therapeutic Dose of Warfarin`), 
         gender = as.factor(Gender)) %>% 
  select(1, 5:7) %>% 
  filter(gender != "NA") %>% 
  drop_na()

data should have appeared in your Global Environment (in the upper right side of the RStudio screen)

After you load data, always check it out to make sure you called what you meant to…I like skim or glimpse for this

skim(data)
Table 1: Data summary
Name data
Number of rows 4443
Number of columns 4
_______________________
Column type frequency:
character 1
factor 1
numeric 2
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
PharmGKB Subject ID 0 1 11 11 0 4443 0

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
gender 0 1 FALSE 2 mal: 2637, fem: 1806, NA: 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
height 0 1 168.06 10.84 124.97 160.02 167.89 176.02 202 ▁▂▇▆▁
dose 0 1 31.23 17.06 2.10 20.00 28.00 39.97 315 ▇▁▁▁▁ 
glimpse(data)
Rows: 4,443
Columns: 4
$ `PharmGKB Subject ID` <chr> "PA135312261", "PA135312262", "PA135312263", "P…
$ height                <dbl> 193.040, 176.530, 162.560, 182.245, 167.640, 17…
$ dose                  <dbl> 49, 42, 53, 28, 42, 49, 42, 71, 18, 17, 97, 49,…
$ gender                <fct> male, female, female, male, male, male, male, m…

Check for correlation

data %>% get_correlation(dose ~ height, na.rm = T)
# A tibble: 1 x 1
    cor
  <dbl>
1 0.315

Just to get an idea of the linear relationship….there is about 30% correlation here between our outcome variable and the continous predictor, height.

3. Check your assumptions

There are a number of assumptions that need to be correct in order to properly use multiple regression.

  1. Independence of observations

Independence of observations means each participant is only counted as one observation. The statistical assumption of independence of observations stipulates that all participants in a sample are only counted once. This is satisfied if we’re using one observation per person.

  1. Normality

Use hist() to test the dependent varible for a normal distribution.

hist(data$dose)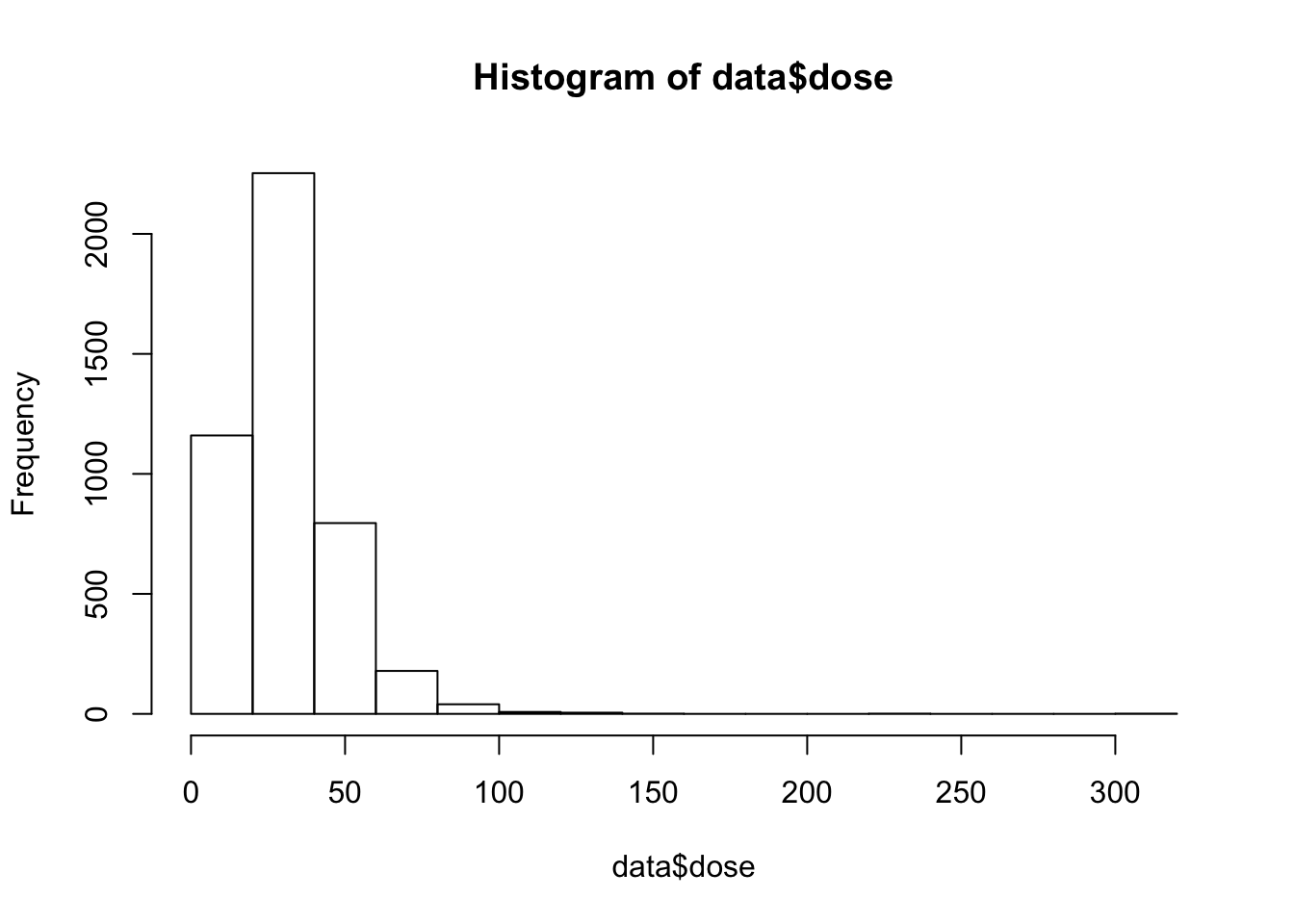

This distrubtion is a lil’ skewed and we should log transform the data.

data$outcome = log(data$dose)

and re-plot…

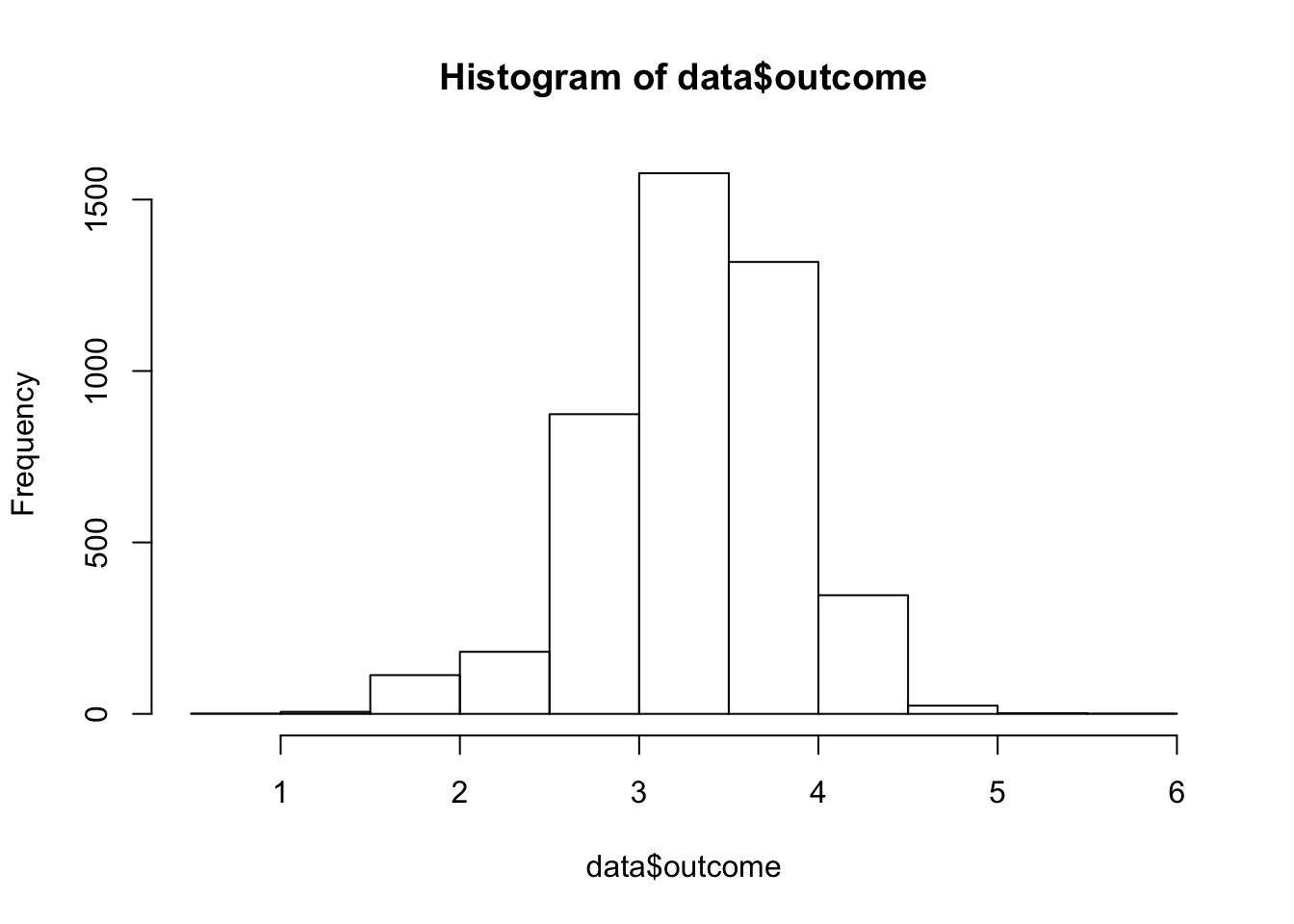
This plot is much more bell-shaped and we can move on.

  1. Linearity should be assessed using scatterplots of the outcome (dependent) variable with each of the included predictors (independent variables).
data %>% filter(gender != "NA") %>% ggplot(aes(outcome, height, group = gender, color = gender)) + geom_point() +
  geom_parallel_slopes(se = F) +
  theme_bw()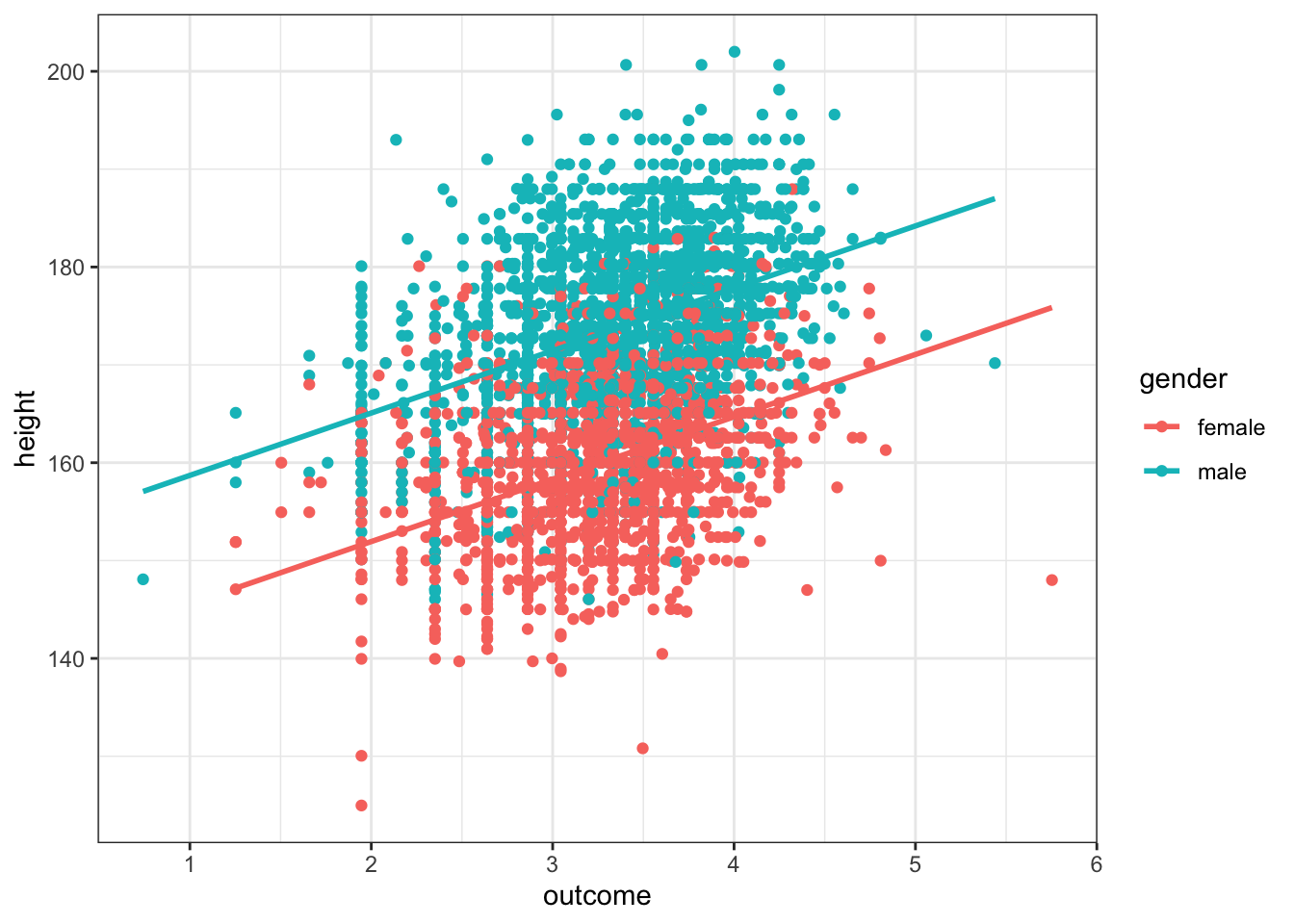

In this plot we’ve visualized both the numeric predictor variable, height, and the factor predictor, gender, by setting the aesthetics for each of these variables.

  1. Homoscedasticity The fourth assumption is equal variance among the residuals…which we will test after running the model by plotting residuals.

4. Run the model

Linear regression syntax is super straighforward in R. The model is given as outcome ~ predictor + predictor and you can call it with the lm() function. I’ve included the wrapper summary() so we can get the statistics back from the regression. Alternatively, use the moderndive package and get_regression_table() to get the same output.

fit = lm(data = data, outcome ~ gender + height)
summary(fit)

Call:
lm(formula = outcome ~ gender + height, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.95202 -0.28410  0.03265  0.32105  2.78849 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.7451039  0.1385046   -5.38 7.85e-08 ***
gendermale  -0.2720412  0.0190291  -14.30  < 2e-16 ***
height       0.0250611  0.0008626   29.05  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4912 on 4440 degrees of freedom
Multiple R-squared:  0.163, Adjusted R-squared:  0.1626 
F-statistic: 432.3 on 2 and 4440 DF,  p-value: < 2.2e-16

or use moderndive…

get_regression_table(fit)
# A tibble: 3 x 7
  term       estimate std_error statistic p_value lower_ci upper_ci
  <chr>         <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept    -0.745     0.139     -5.38       0   -1.02    -0.474
2 gendermale   -0.272     0.019    -14.3        0   -0.309   -0.235
3 height        0.025     0.001     29.1        0    0.023    0.027

5. Plot Residuals

Super important to come back and check homoscedasticity (equal variance) of the residuals. Do this by plotting the same lm() used previously. Residuals are calculated from model error and you can think about them as unexplained variance.

par(mfrow = c(2,2)) ## show 4 plots at once
plot(fit) ## plot residuals

What you want here is, basically, horizontal lines centered around 0 for each of the plots except the Q-Q plot which should follow along the theoretical quantiles.

data$predicted <- predict(fit)   # Save the predicted values
data$residuals <- residuals(fit) # Save the residual values

# Quick look at the actual, predicted, and residual values

data %>% select(outcome, predicted, residuals) %>% head()
# A tibble: 6 x 3
  outcome predicted residuals
    <dbl>     <dbl>     <dbl>
1    3.89      3.82    0.0712
2    3.74      3.68    0.0587
3    3.97      3.33    0.641 
4    3.33      3.55   -0.218 
5    3.74      3.18    0.554 
6    3.89      3.44    0.453

Here’s another, much prettier plot of residuals.

data %>% 
  sample_frac(.5) %>% 
  gather(key = "gender", value = "x", -outcome, -predicted, -`PharmGKB Subject ID`, -residuals, -dose, -height) %>%  # Get data into shape
  ggplot(aes(x = height, y = outcome)) +  
  geom_segment(aes(xend = height, yend = predicted), alpha = .2) +
  geom_point(aes(color = residuals)) +
  scale_color_gradient2(low = "blue", mid = "white", high = "red") +
  guides(color = FALSE) +
  geom_point(aes(y = predicted), color = "gray", alpha = .5) +
  facet_grid(~ x, scales = "free_x") +  # Split panels here by `iv`
  theme_gray()

That’s really the basics of performing a linear regression in R.

biostatistics R Markdown
Heidi E. Steiner
Heidi E. Steiner
Senior Clinical Data Scientist

I love coding in R, biostatistics, and reproducible clinical research.

Related